segunda-feira, 24 de setembro de 2018
quarta-feira, 29 de agosto de 2018
terça-feira, 12 de setembro de 2017
LISTA DE EXERCÍCIOS SOBRE REGRA DE TRÊS SIMPLES
Segue abaixo uma lista de exercícios com problemas envolvendo regra de três simples direta e inversa.
1) Um automóvel fez 180
km com 15 l de álcool. Calcule quantos litros de álcool esse automóvel gastaria
para percorrer 210 km.
2) Uma máquina produz
75 litros de sorvete em 30 minutos. Quantos litros de sorvete seriam produzidos
em 2 horas por essa máquina?
3) Sabendo que 1200
frangos consomem 90 kg de ração por dia, quantos quilogramas de ração 2000
frangos consumirão por dia?
4) Com 10 l de óleo de
copaíba, árvore nativa de Amazônia, uma caminhão consegue andar 80km. Quantos litros
deverão ser utilizados num percurso de 200 km?
5) Um aparelho consegue
irrigar 2 ha (hectares) em 40 minutos. Quantos hectares serão irrigados em 2
horas por esse aparelho?
6) A comida que restou
para 3 náufragos seria suficiente para alimentá-los por 12 dias. Um deles
resolveu saltar e tentar chegar ao continente nadando. Com um náufragos a
menos, qual será a duração dos alimentos?
7) Se 12 operários
levam 18 dias para realizar determinado trabalho, quantos operários realizarão
este trabalho em 6 dias?
8) O Brasil vem se destacando com um dos países
que mais reciclam latas de alumínio. Em 2007, por exemplo, foram recicladas
cerca de 96,5% da latas comercializadas no Brasil, o que corresponde a
aproximadamente 12 bilhões de unidades. A reciclagem traz benefícios a diversos
setores da sociedade, pois gera empregos, movimenta a economia e preserva o
meio ambiente. Em uma usina de reciclagem são necessárias em média 600 latas
para se obter 8 quilos de alumínio. Quantas latas são necessárias para obter
150 quilos de alumínio?
9) Um pintor utilizou
18 litros de tinta para pintar 60 m2. Quantos litros de tinta serão
necessários para pintar 450 m2, da mesma forma como foram pintados
os 60 m2?
10) Márcia leu um livro
em 4 dias, lendo 15 páginas por dia. Se tivesse lido 6 páginas por dia, em
quantos dias ela teria lido o mesmo livro?
11) Uma equipe de 25
pessoas demora 36 dias para reflorestar uma área devastada. Quantas pessoas,
com este mesmo rendimento, são necessárias para reflorestar essa área em 12
dias?
12) A cana-de-açúcar é
uma fonte de energia utilizada em alguns casos na substituição de petróleo. A
energia contida em 5 toneladas de cana-de-açúcar equivale a 6 barris de
petróleo. Quantos barris de petróleo equivalem a 15 toneladas de
cana-de-açúcar?
13 - Um galpão pode ser
construído em 48 dias por 7 pedreiros que trabalham num certo ritmo. Como ele
deve ser construído em 2 semanas, no mesmo ritmo de trabalho, quantos pedreiros
serão necessários?
Segue um link para estudar o assunto caso tenha dúvida: http://www.somatematica.com.br/fundam/regra3s.php
Segue um link para estudar o assunto caso tenha dúvida: http://www.somatematica.com.br/fundam/regra3s.php
Boa sorte a Todos
Professor Neurisvaldo
segunda-feira, 11 de setembro de 2017
LISTA DE EXERCÍCIOS ONLINE-REGRA DE TRÊS SIMPLES
Acesse o link: http://rachacuca.com.br/quiz/30845/regra-de-tres-simples/
Para fazer exercícios sobre regra de três simples.
Para fazer exercícios sobre regra de três simples.
terça-feira, 23 de maio de 2017
Geometria Analítica - Hora de Estudar
Os estudos em Geometria Analítica possibilitam a
relação entre a Álgebra e a Geometria, abrangendo situações em que são
envolvidos ponto, reta e figuras espaciais.
A distância entre dois pontos é determinada pela Geometria Analítica,
responsável por estabelecer relações entre fundamentos geométricos e
algébricos. As relações são intituladas com base num sistema de coordenadas
cartesianas, que é constituído de dois eixos perpendiculares enumerados.
No plano cartesiano, qualquer ponto possui uma coordenada de
localização, basta identificar o ponto e observar os valores primeiramente em
relação ao eixo horizontal x (abscissa) e posteriormente em relação ao eixo
vertical y (ordenada).
Nesse sistema de coordenadas podemos demarcar dois pontos e
determinar a distância entre eles. Observe:
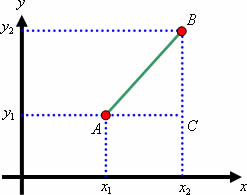
Observe que o triângulo formado é retângulo de catetos AC e BC e
hipotenusa AB. Se aplicarmos o Teorema de Pitágoras nesse triângulo
determinando a medida da hipotenusa estaremos também calculando a distância
entre os pontos A e B. Vamos aplicar as propriedades da relação de Pitágoras no
triângulo ABC, originando a expressão matemática responsável pela determinação
da distância entre dois pontos em função de suas coordenadas.
O Teorema de Pitágoras diz: “A soma dos quadrados dos catetos é
igual ao quadrado da hipotenusa”. No triângulo ABC temos que:
Cateto
AC = x2 – x1
Cateto
BC = y2 – y1
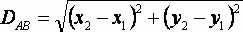
Exemplo
Calcule a distância
entre os pontos P(-2,3) e Q(-5,-9).
x1: -2
x2: -5
y1: 3
y2: -9
.jpg)
PONTO MÉDIO DE UM SEGMENTO
Por ser um “pedaço” de uma reta podemos medir o seu comprimento (distância entre dois pontos de uma reta), assim possuindo seu ponto médio (ponto que separa o segmento ao meio).
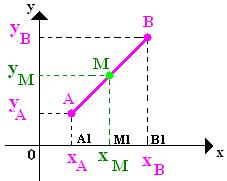
Exemplo 1
Dados os pontos P(5,1) e Q(–2,–9), determine as coordenadas do ponto médio do segmento PQ.
xM = [5 + (–2)] / 2
xM = (5 – 2) / 2
xM = 3/2
yM = [1 + (–9)] / 2
yM = (1 – 9) / 2
yM = –8/2
yM = –4
Portanto, M(3/2, –4) é o ponto médio do segmento PQ.
Por ser um “pedaço” de uma reta podemos medir o seu comprimento (distância entre dois pontos de uma reta), assim possuindo seu ponto médio (ponto que separa o segmento ao meio).
Exemplo 1
Dados os pontos P(5,1) e Q(–2,–9), determine as coordenadas do ponto médio do segmento PQ.
xM = [5 + (–2)] / 2
xM = (5 – 2) / 2
xM = 3/2
yM = [1 + (–9)] / 2
yM = (1 – 9) / 2
yM = –8/2
yM = –4
Portanto, M(3/2, –4) é o ponto médio do segmento PQ.
Lista de exercícios com gabarito sobre Geometria Analítica.
Identificar a localização de pontos no plano cartesiano:
01 - Exercícios Plano cartesiano;
02 - Exercícios Extra Geometria Analítica;
01 - Exercícios Plano cartesiano;
02 - Exercícios Extra Geometria Analítica;
terça-feira, 11 de abril de 2017
MEDIDAS DE TENDÊNCIA CENTRAL: MÉDIA, MODA E MEDIANA
MÉDIA ARITMÉTICA
A Média é a mais
importante das Medidas de Posição e saber calculá-la é simplesmente essencial
para qualquer prova de Estatística.
Quando a
questão pedir que se calcule a Média, simplesmente isso, estaremos tratando da Média Aritmética. Na verdade, há outros
dois tipos de Média: a Geométrica e a Harmônica. Como estas duas últimas
costumam ser quase sempre ignoradas nas provas, embora presentes no programas
dos editais, as explicaremos mais adiante, em uma aula à parte.
Segue o link com o documento sobre Média.
MODA
#
Conceito:
Na linguagem coloquial (as alunas o sabem
perfeitamente!), moda é algo que está em evidência, ou seja, algo que se vê
bastante! Na Estatística, como o próprio nome sugere, a Moda é aquele
elemento que mais vezes aparece no conjunto! (Leia-se: é o elemento de
maior frequência). Sua determinação é bastante simples, como se verá adiante.
Segue o link com o documento sobre Moda.
MEDIANA –
PARTE 01
# Observação Preliminar:
Desde que iniciamos o estudo da Média e da Moda, estamos sempre
as chamando de Medidas de Posição! E de fato, o são; da mesma forma que
a Mediana! Ocorre que as Medidas de Posição não se restringem a estas três,
cujo estudo estamos prestes a encerrar. Na verdade, a Média, a Moda e a Mediana
fazem parte de um grupo de Medidas de Posição, o qual chamamos de Medidas de
Tendência Central!
Segue o link com o documento sobre Mediana Parte 01.
MEDIANA
– PARTE 02
# Determinação da Mediana
–
à
Mediana para Distribuição de Frequências:
Vimos que, quando íamos procurar a Mediana
no rol e nos dados tabulados, tínhamos sempre a preocupação de saber se o n
(número de elementos do conjunto) era par ou ímpar! Essa preocupação deixa de
existir no cálculo da Mediana para a distribuição de frequências.
Aqui, teremos simplesmente que aplicar a
fórmula da Mediana, cujos elementos serão extraídos de uma determinada classe
da distribuição: a chamada Classe Mediana.
Daí, basicamente o que precisamos fazer para
determinar a Mediana de uma distribuição será:
1o) Descobrir quem é a Classe
Mediana; e
2o) Aplicar a fórmula da Mediana
para distribuição de frequências!
Segue o link com o documento sobre Mediana Parte 02.
Segue o link com uma lista de exercícios de revisão.
segunda-feira, 10 de abril de 2017
segunda-feira, 11 de abril de 2016
ESTUDO DE FUNÇÕES
Dados dois conjuntos A e B não vazios, uma função f de A em B é uma relação que associa a cada elemento x pertencente a A
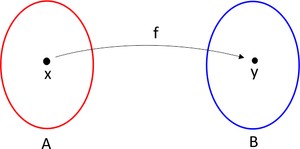

Vejamos agora alguns Objetos Educacionais sobre funções:
- Objeto Educacional 01:
- Objeto Educacional 02:
segunda-feira, 29 de fevereiro de 2016
terça-feira, 17 de novembro de 2015
segunda-feira, 31 de agosto de 2015
segunda-feira, 24 de agosto de 2015
sexta-feira, 31 de julho de 2015
POLINÔMIOS
No 3º Bimestre da 3ª Série do Ensino Médio será trabalhado Polinômios:
Equação Polinomial
Relação de Girard:
Para exemplificar o conteúdo segue os slides e um livro sobre o conteúdo: Clique no link para fazer o download do Material de estudo:
Livro sobre Polinômios - Material Completo sobre Polinômios;
Polinômios I - Slide;
Polinômio II - Slide;
COMPETÊNCIAS
ü Permitir
que o aluno traduza e generalize padrões aritméticos, estabeleça relações entre
grandezas variáveis, compreenda e utilize diversos significados do uso da simbologia
em situações novas e, muitas vezes, inesperadas, bem como serva de ferramenta
para resolver problemas que tenham aplicações diretas.
HABILIDADES
ü Estabelecer
e aplicar relações entre coeficientes e raízes de polinômios.
ü Efetuar
operações (adição, subtração, multiplicação e divisão) de polinômios.
ü Determinar
as raízes de uma equação algébrica, bem como as suas multiplicidades.
ü Relacionar
o estudo de polinômios e equações polinomiais com o estudo de funções.
ü Aplicar
os teoremas do resto e de D’Alembert, o dispositivo de BriottRuffini, o teorema
fundamental da álgebra e as relações de Girard.
ü Escrever
uma equação para representar uma relação entre duas variáveis.
ü Escrever
uma sentença, dada uma equação linear simples, em duas variáveis (forma pictórica).
CONTEÚDOS
Polinômios:
ü Função
Polinomial
ü Operações
com Polinômio
ü Teorema
do Resto
ü Teorema
de D’ Alembert
ü Algoritmo
de BriotRuffini
ü Raízes
de uma Equação Polinomial
ü Soma
e/ou Produto das Raízes de uma Equação Polinomial
ü Equações
Algébricas:
ü Raiz
ou zero da equação
ü Teorema
ü fundamental
da álgebra
ü Teorema
da decomposição
ü Multiplicidade
de uma raiz
ü Raízes nulas
e complexas
Assinar:
Comentários
(
Atom
)




























