Três pontos estão
alinhados se, e somente se, pertencerem à mesma reta.
.jpg)
Para verificarmos se
os pontos estão alinhados, podemos utilizar a construção gráfica determinando
os pontos de acordo com suas coordenadas posicionais. Outra forma de determinar
o alinhamento dos pontos é através do cálculo do determinante pela regra de Sarrus
envolvendo a matriz das coordenadas.
.jpg)
Exemplo 1. Verifique se os pontos A(5, 5), B(1, 3) e C(0,
5) estão alinhados.
Solução: devemos fazer
o cálculo do determinante das coordenadas dos pontos A, B e C e verificar se o
resultado é igual a zero.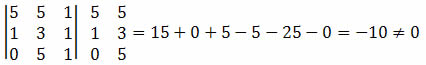
Exemplo 2. Dados os pontos A (2, 5), B (3, 7) e C (5, 11), vamos determinar se estão alinhados.
.jpg)
Somatório diagonal principal – Somatório diagonal secundária
(14 + 25 + 33) – (35 + 22 + 15)
72 – 72 = 0
Os pontos somente estarão alinhados se o determinante da matriz quadrada calculado pela regra de Sarrus for igual a 0.
Equação geral da Reta
Para determinarmos a equação geral de uma reta utilizamos os conceitos relacionados a matrizes. Na determinação da equação na forma ax + by + c = 0 aplicamos a regra de Sarrus utilizada na obtenção do discriminante de uma matriz quadrada de ordem 3 x 3. Para utilizarmos uma matriz nessa determinação da equação geral devemos ter no mínimo dois pares ordenados (x,y) dos possíveis pontos alinhados, por onde a reta irá passar. Observe a matriz geral da determinação da equação geral:
.jpg)
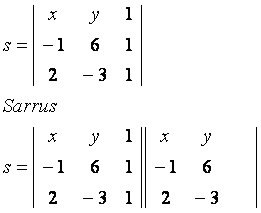
Para determinarmos a equação geral de uma reta utilizamos os conceitos relacionados a matrizes. Na determinação da equação na forma ax + by + c = 0 aplicamos a regra de Sarrus utilizada na obtenção do discriminante de uma matriz quadrada de ordem 3 x 3. Para utilizarmos uma matriz nessa determinação da equação geral devemos ter no mínimo dois pares ordenados (x,y) dos possíveis pontos alinhados, por onde a reta irá passar. Observe a matriz geral da determinação da equação geral:
.jpg)
Vamos considerar o
ponto genérico P(x, y), pertencente à reta s que passa pelos pontos A(–1, 6) e
B(2, –3). Observe a matriz construída com as coordenadas oferecidas:
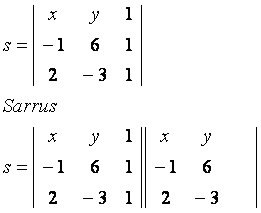
Diagonal principal
x * (–6) * 1 = 6x
y * 1 * 2 = 2y
1 * (–1) * (–3) = 3
Diagonal secundária
1* 6 * 2 = 12
x * 1 * (–3) = –3x
y * (–1) * 1 = –y
(6x + 2y + 3) – (12 –
3x – y) = 0
6x + 2y + 3 – 12 +
3x + y = 0
9x + 3y – 9 = 0 (dividindo a equação por 3)
3x + y – 3 = 0













